item a) e b)
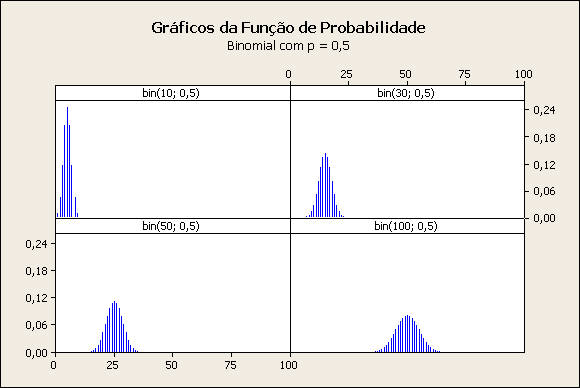
Comentário: Caso p = 0,5
Os gráficos de probabilidade são simétricos em relação à média da distribuição, np. A variância cresce à medida que n aumenta.
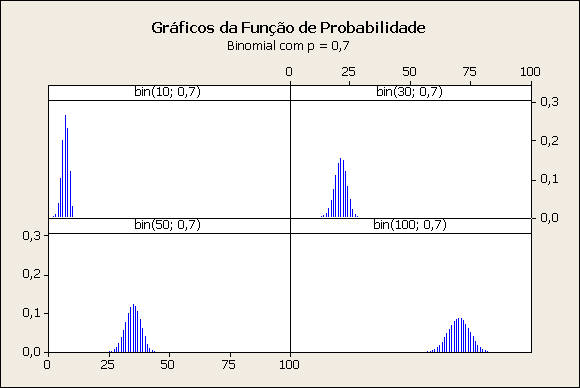
Comentário: Caso p = 0,7
O gráfico com n=10 apresenta uma certa assimetria. Os demais gráficos de probabilidade são simétricos em relação à média da distribuição, np. Considerando os quatro gráficos, a variância cresce à medida que n aumenta.
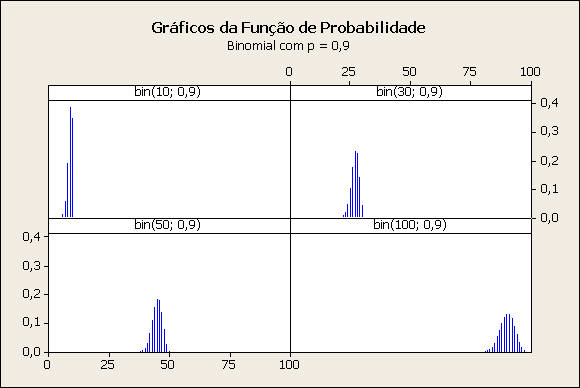
Comentário: Caso p = 0,9
Os gráficos com n = 10, 30 e 50 apresentam alguma assimetria. Os demais gráficos de probabilidade são simétricos em relação à média da distribuição, np. Considerando os quatro gráficos, a variância cresce à medida que n aumenta.
item c) e d)
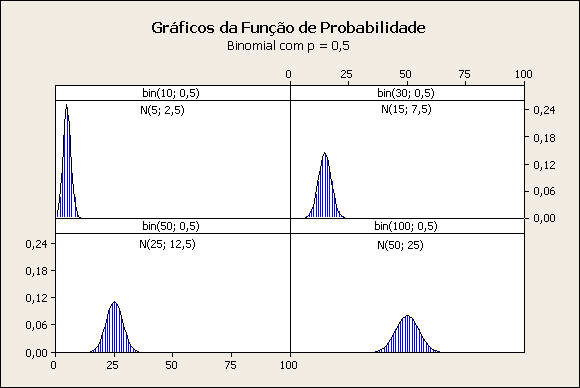
Comentário: Caso p = 0,5
Embora expressando grandezas diferentes (probabilidade e densidade de probabilidade), aparentemente a função de densidade de probabilidade da distribuição normal escolhida se ajusta razoavelmente ao formato do gráfico de probabilidade da distribuição binomial.
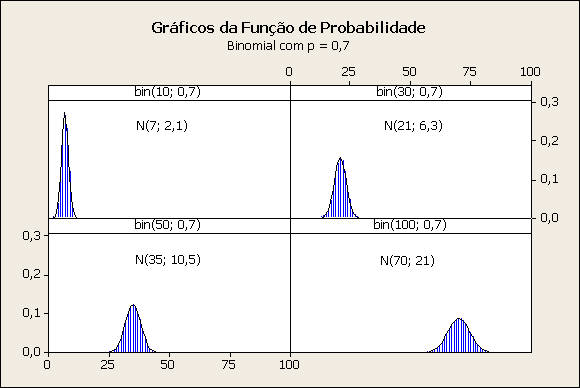
Comentário: Caso p = 0,7
Com a ressalva sobre a natureza das funções, apontada no comentário anterior, verifica-se que a função de densidade da distribuição normal se ajusta razoavelmente ao formato do gráfico de probabilidade da binomial. O gráfico para n = 10 deveria ser em maior escala para permitir uma verificação de seu ajuste, pois, notamos uma certa assimetria na binomial.
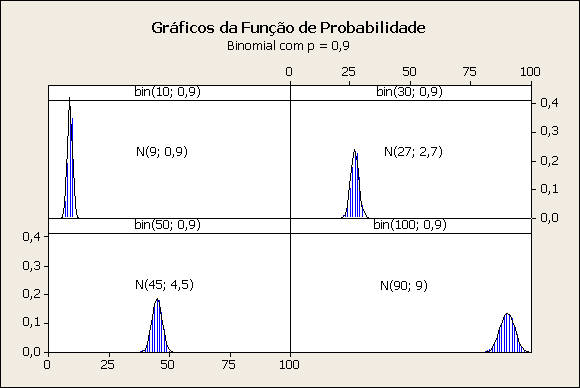
Comentário: Caso p = 0,9
Com a ressalva sobre a natureza das funções, apontada nos comentários anteriores, verifica-se que a função de densidade da distribuição normal apresenta desvios com o formato do gráfico de probabilidade da binomial nos casos de n= 10 e , n = 30. O gráfico para n = 50 deveria ser em maior escala para permitir uma verificação de seu ajuste, pois, notamos anteriormente uma certa assimetria na binomial. No caso em que n = 100, o ajuste aparenta ser razoável.
Exercício 2:
item a)
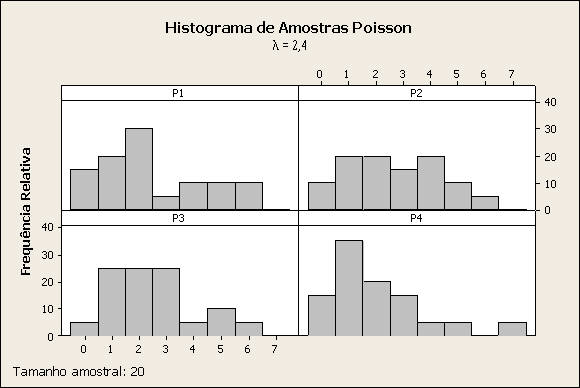
item b)
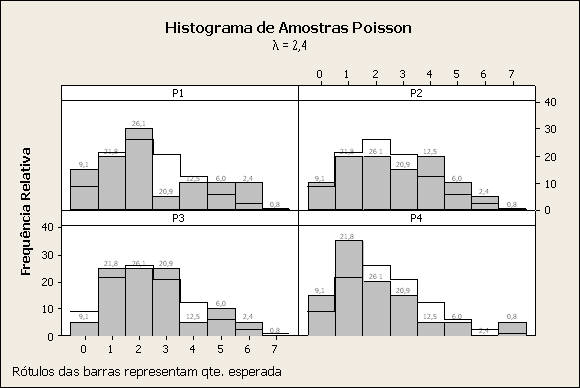
Comentário: O histograma está em freqüência relativa, tendo sido comparado com os valores percentuais exatos de uma distribuição de probabilidade de Poisson, com parãmetro 2,4. Verificam-se desvios entre os valores amostrais e os valores teóricos.
item c)
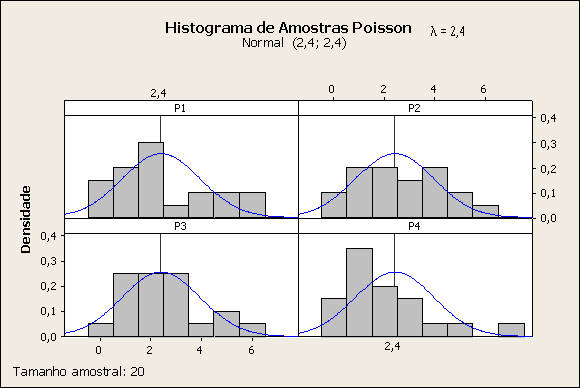
Comentário: Há amostras cujo histograma não é simétrico, o que por si só inviabiliza uma aproximação pela normal. Seria interessante uma comparação das medianas e médias, identificando-as no gráfico para facilitar uma melhor análise empírica.
item d)
Descriptive Statistics: P1; P2; P3; P4
Variable Mean Variance
P1 2,450 3,734
P2 2,650 2,976
P3 2,500 2,474
P4 2,000 3,158
Distribuição exata: POisson (2,4)
Media: 2,4
Variância: 2,4
Comentário: As médias estão razoavelmente próximas, considerados seus coeficientes de variação. As variâncias amostrais mostram-se maiores que a variância exata.
Exercício 3:
item a)
Descriptive Statistics: E1; E2; E3
Variable Mean StDev
E1 123,4 111,1
E2 104,4 92,3
E3 110,7 96,3
Distribuição exata: expondencial, com lambda = 1/128
Média: 128
Desvio Padrão: 128
Comentário: O s valores da média amostral estão bastante próximos da média verdadeira, considerando desvio-padrão como unidade de medida. Há maior diferença nos desvios-padrão amostrais.
item b)
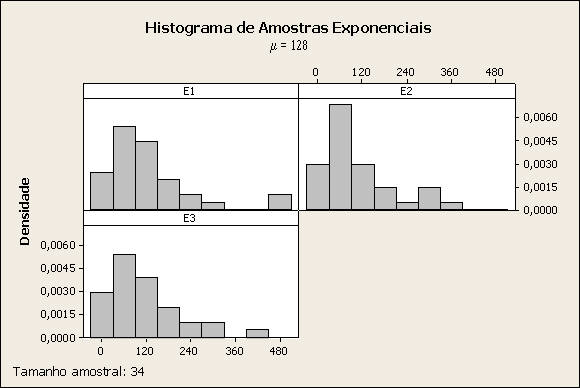
Comentário: O .
item c)
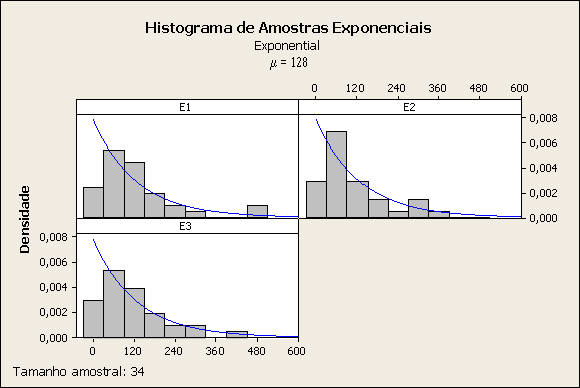
Comentário: A comparação foi efetuada na mesma grandeza (densidade de probabilidade). Distribuição exata bastante próxima dos histogramas, com exceção da região de fronteira, em zero.
Exercício 4:
item a) e b)
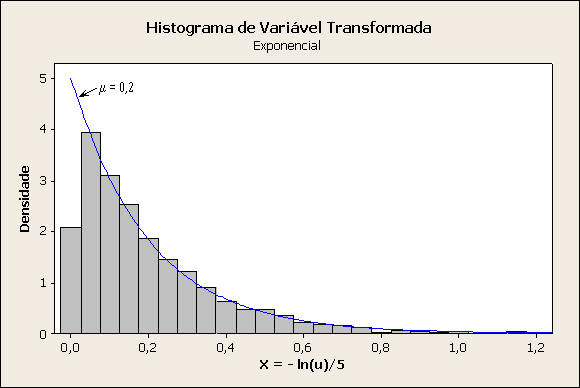
item c)
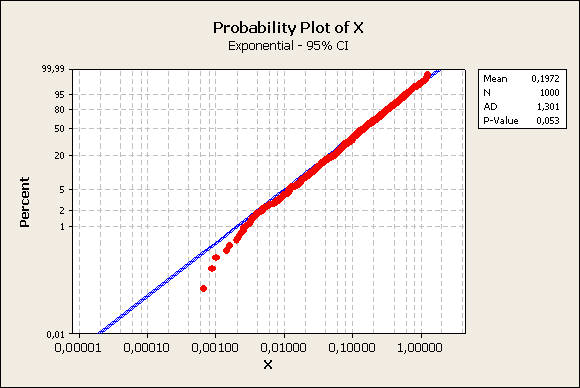
Descriptive Statistics: X
Variable Mean Variance
X 0,19725 0,03479
Valores Exatos da Distribuição Exponencial
Média: 0,2
Variância: 0,04
Comentário: Resultados amostrais da variável transformada bastante próximos de uma distribuição exponencial com média 0,2. O histograma mostra um desvio no ajuste na região da fronteira, alertando-se que o mesmo não está correto, pois a primeira classe considera o zero como ponto médio da classe (assumindo valores negativos) quando se verifica que pela transformação a variável não contempla valores negativos (assim como a exponencial). O ideal seria modificar as classes do histograma para que esta condição fosse respeitada. Pelo Probability Plot (ara uma exponencial) não há evidências amostrais para rejeição da hipótese de que amostra veio de uma distribuição exponencial, embora indique possíveis desvios para os menores valores (aqueles próximos de zero).